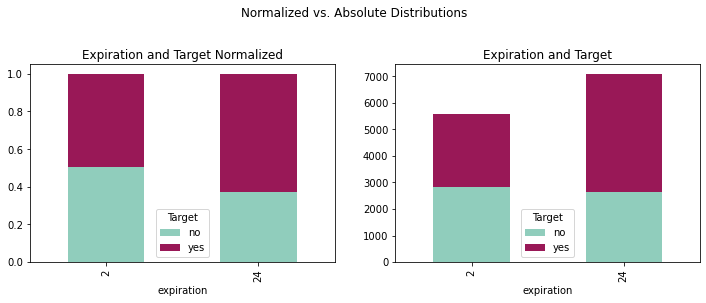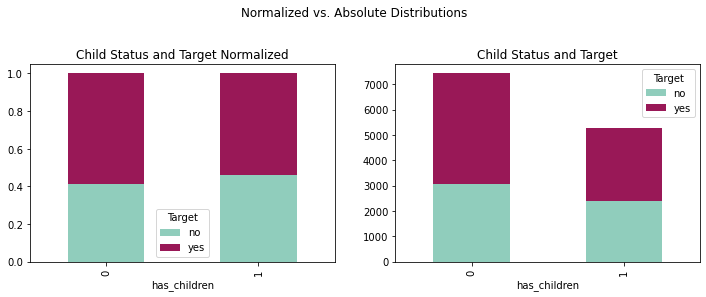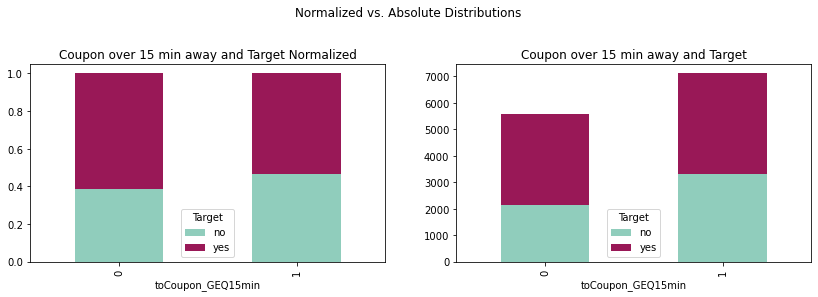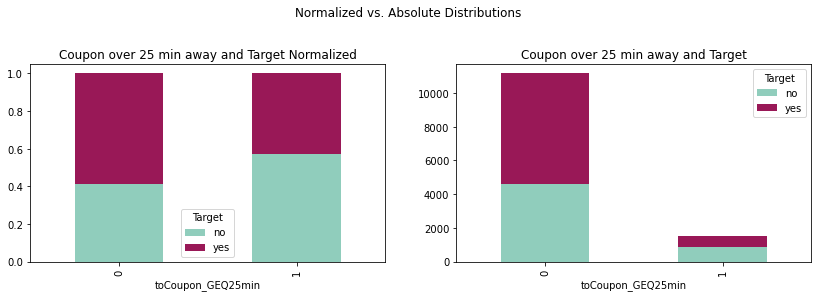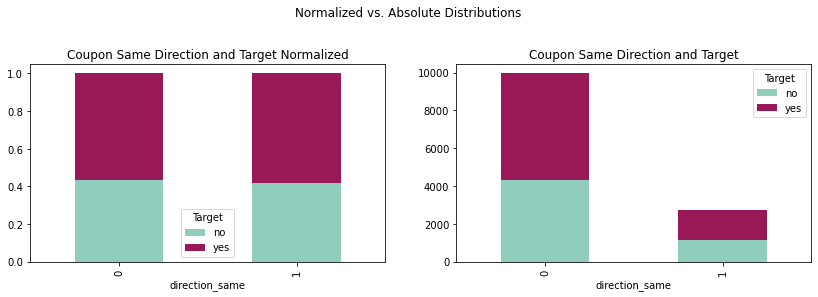Appendix: Exploratory Data Analysis (EDA) and Preprocessing¶
Team 2 - Shpaner, Leonid; Oakes, Isabella, Lucban, Emanuel¶
Loading the requisite libraries
In [1]:
import pandas as pd
import numpy as np
import json
import matplotlib.pyplot as plt
import seaborn as sns
import plotly as ply
import random
from sklearn.preprocessing import OneHotEncoder, OrdinalEncoder, LabelEncoder, \
StandardScaler, Normalizer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import BayesianRidge, LogisticRegression
# Enable Experimental
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import SimpleImputer, IterativeImputer
from sklearn import tree
import statsmodels.api as sm
from scipy import stats
from sklearn.metrics import confusion_matrix, plot_confusion_matrix,\
classification_report,accuracy_score
from sklearn import linear_model
from sklearn.svm import SVC
import warnings
warnings.filterwarnings('ignore')
Reading in and Inspecting the dataframe
In [2]:
coupons_df = pd.read_csv('https://archive.ics.uci.edu/ml/\
machine-learning-databases/00603/in-vehicle-coupon-recommendation.csv')
coupons_df.head()
Out[2]:
In [3]:
coupons_df.dtypes
Out[3]:
In [4]:
null_vals = pd.DataFrame(coupons_df.isna().sum(), columns=['Null Count'])
null_vals['Null Percent'] = (null_vals['Null Count'] / coupons_df.shape[0]) * 100
null_vals
Out[4]:
EDA - Discovery¶
Renaming Columns
In [5]:
# Renaming the passanger column to 'passenger'
coupons_df = coupons_df.rename(columns={'passanger':'passenger'})
# Renaming the 'Y' column as our Target
coupons_df = coupons_df.rename(columns={'Y':'Target'})
# Binarizing Target Variable
coupons_df['Target'] = coupons_df['Target'].map({1 : 'yes', 0 : 'no'})
# Creating a new column of dummy var. for Binary Target (Response)
coupons_df['Response'] = coupons_df['Target'].map({'yes':1, 'no':0})
Removing Highly Correlated Predictors
In [6]:
correlation_matrix = coupons_df.corr()
correlated_features = set()
for i in range(len(correlation_matrix .columns)):
for j in range(i):
if abs(correlation_matrix.iloc[i, j]) > 0.8:
colname = correlation_matrix.columns[i]
correlated_features.add(colname)
print(correlated_features)
Mapping Important Categorical Features to Numerical Ones
In [7]:
print(coupons_df['education'].unique())
In [8]:
coupons_df['educ. level'] = coupons_df['education'].map(\
{'Some High School':1,
'Some college - no degree':2,
'Bachelors degree':3, 'Associates degree':4,
'High School Graduate':5,
'Graduate degree (Masters or Doctorate)':6})
In [9]:
# create new variable 'avg_income' based on income
inc = coupons_df['income'].str.findall('(\d+)')
coupons_df['avg_income'] = pd.Series([])
for i in range(0,len(inc)):
inc[i] = np.array(inc[i]).astype(np.float)
coupons_df['avg_income'][i] = sum(inc[i]) / len(inc[i])
print(coupons_df['avg_income'])
In [10]:
# Creating new age range column
print(coupons_df['age'].value_counts())
coupons_df['Age Range'] = coupons_df['age'].map({'below21':'21 and below',
'21':'21-25','26':'26-30',
'31':'31-35','36':'36-40',
'41':'41-45','46':'46-50',
'50plus':'50+'})
In [11]:
# Creating new age group column based on ordinal values
print(coupons_df['age'].value_counts())
coupons_df['Age Group'] = coupons_df['age'].map({'below21':1,
'21':2,'26':3,
'31':4,'36':5,
'41':6,'46':6,
'50plus':7})
In [12]:
# Numericizing Age variable by adding new column: 'ages'
coupons_df['ages'] = coupons_df['age'].map({'below21':20,
'21':21,'26':26,
'31':31,'36':36,
'41':41,'46':46,
'50plus':65})
In [13]:
# Changing coupon expiration to uniform # of hours
coupons_df['expiration'] = coupons_df['expiration'].map({'1d':24, '2h':2})
In [14]:
# Convert time to 24h military time
def convert_time(x):
if x[-2:] == "AM":
return int(x[0:-2]) % 12
else:
return (int(x[0:-2]) % 12) + 12
coupons_df['time'] = coupons_df['time'].apply(convert_time)
Selected Features by Target Response¶
In [15]:
print("\033[1m"+'Target Outcome by Age (Maximum Values):'+"\033[1m")
def target_by_age():
target_yes = coupons_df.loc[coupons_df.Target == 'yes'].groupby(
['Age Range'])[['Target']].count()
target_yes.rename(columns={'Target':'Yes'}, inplace=True)
target_no = coupons_df.loc[coupons_df.Target == 'no'].groupby(
['Age Range'])[['Target']].count()
target_no.rename(columns={'Target':'No'}, inplace=True)
target_age = pd.concat([target_yes, target_no], axis = 1)
target_age['Yes'] = target_age['Yes'].fillna(0)
target_age['No'] = target_age['No'].fillna(0)
target_age
max = target_age.max()
print(max)
target_age.loc['Total'] = target_age.sum(numeric_only=True, axis=0)
target_age['% of Total'] = round((target_age['Yes'] / (target_age['Yes'] \
+ target_age['No']))* 100, 2)
return target_age.style.format("{:,.0f}")
target_by_age()
Out[15]:
In [16]:
print("\033[1m"+'Target Outcome by Income (Maximum Values):'+"\033[1m")
def target_by_income():
target_yes = coupons_df.loc[coupons_df.Target == 'yes'].\
groupby(['avg_income'])[['Target']].count()
target_yes.rename(columns={'Target':'Yes'}, inplace=True)
target_no = coupons_df.loc[coupons_df.Target == 'no'].\
groupby(['avg_income'])[['Target']].count()
target_no.rename(columns={'Target':'No'}, inplace=True)
target_inc = pd.concat([target_yes, target_no], axis = 1)
target_inc['Yes'] = target_inc['Yes'].fillna(0)
target_inc['No'] = target_inc['No'].fillna(0)
target_inc
max = target_inc.max()
print(max)
target_inc.loc['Total'] = target_inc.sum(numeric_only=True, axis=0)
target_inc['% of Total'] = round((target_inc['Yes'] / (target_inc['Yes'] \
+ target_inc['No']))* 100, 2)
return target_inc.style.format("{:,.0f}")
target_by_income()
Out[16]:
Selected Features' Value Counts¶
In [17]:
age_count = coupons_df['Age Range'].value_counts().reindex(["21 and below",
"21-25", "26-30",
"31-35","36-40",
"41-45", "46-50",
"50+"])
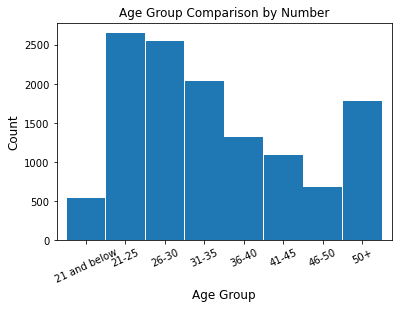
fig = plt.figure()
age_count.plot.bar(x ='lab', y='val', rot=0, width=0.98)
plt.title ('Age Group Comparison by Number', fontsize=12)
plt.xlabel('Age Group', fontsize=12)
plt.ylabel('Count', fontsize=12); plt.xticks(rotation = 25)
plt.show()
age_count
Out[17]:
In [18]:
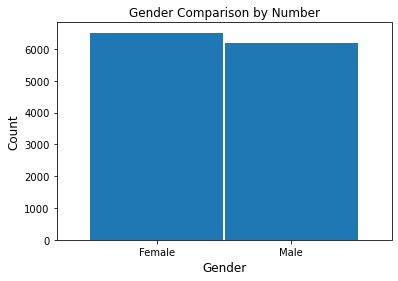
gender_count = coupons_df['gender'].value_counts()
fig = plt.figure()
gender_count.plot.bar(x ='lab', y='val', rot=0, width=0.99)
plt.title ('Gender Comparison by Number', fontsize=12)
plt.xlabel('Gender', fontsize=12)
plt.ylabel('Count', fontsize=12)
plt.show()
gender_count
Out[18]:
In [19]:
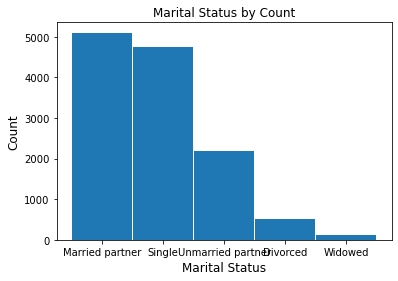
marital_coupons = coupons_df['maritalStatus'].value_counts()
fig = plt.figure()
marital_coupons.plot.bar(x ='lab', y='val', rot=0, width=0.98)
plt.title ('Marital Status by Count', fontsize=12)
plt.xlabel('Marital Status', fontsize=12)
plt.ylabel('Count', fontsize=12)
plt.show()
marital_coupons
Out[19]:
In [20]:
print("\033[1m"+'Coupon Summary Statistics:'+"\033[1m")
def coupon_summary_stats():
pd.options.display.float_format = '{:,.2f}'.format
coupon_summary = pd.DataFrame(coupons_df).describe().transpose()
cols_to_keep = ['mean', 'std', 'min', '25%', '50%','75%', 'max']
coupon_summary = coupon_summary[cols_to_keep]
stats_rename = coupon_summary.rename(columns={'count':'Count','min':'Minimum',
'25%':'Q1','50%':'Median','mean':'Mean','75%':
'Q3','std': 'Standard Deviation','max':'Maximum'})
return stats_rename
coupon_summary_stats()
Out[20]:
In [21]:
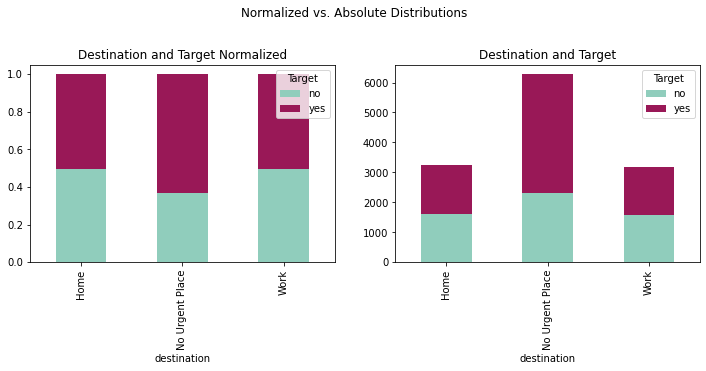
fig = plt.figure(figsize=(12, 8))
ax2 = fig.add_subplot(221); ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
crosstabdest = pd.crosstab(coupons_df['destination'], coupons_df['Target'])
crosstabdestnorm = crosstabdest.div(crosstabdest.sum(1), axis=0)
plotdest = crosstabdest.plot(kind='bar',
stacked=True,
title='Destination and Target',
ax=ax1,
color=['#90CDBC', '#991857'])
plotdestnorm = crosstabdestnorm.plot(kind='bar',
stacked=True,
title='Destination and Target Normalized',
ax=ax2,
color=['#90CDBC', '#991857'])
In [22]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221); ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
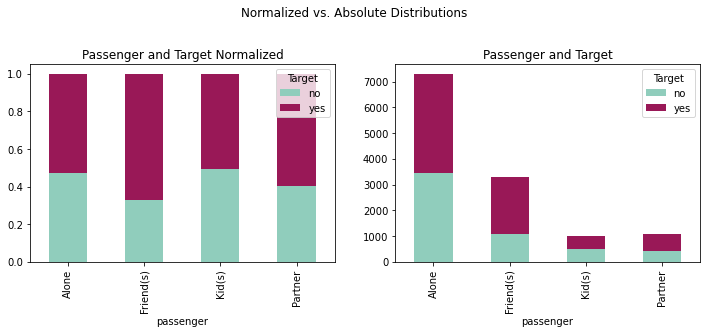
crosstabpass = pd.crosstab(coupons_df['passenger'],coupons_df['Target'])
crosstabpassnorm = crosstabpass.div(crosstabpass.sum(1), axis = 0)
plotpass = crosstabpass.plot(kind='bar', stacked = True,
title = 'Passenger and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plotpassnorm = crosstabpassnorm.plot(kind='bar', stacked = True,
title = 'Passenger and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [23]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
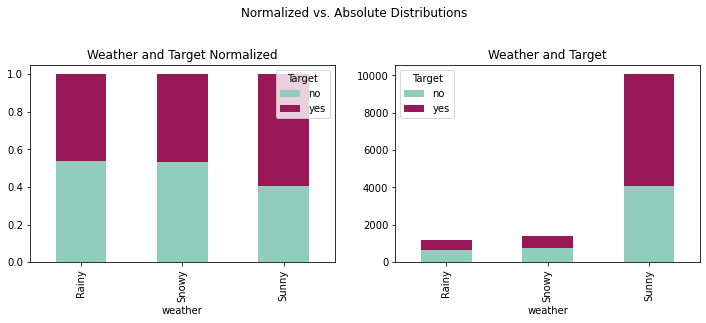
crosstabweat = pd.crosstab(coupons_df['weather'],coupons_df['Target'])
crosstabweatnorm = crosstabweat.div(crosstabweat.sum(1), axis=0)
plotweat = crosstabweat.plot(kind='bar', stacked = True,
title='Weather and Target',
ax=ax1, color=['#90CDBC', '#991857'])
plotweatnorm = crosstabweatnorm.plot(kind='bar', stacked = True,
title='Weather and Target Normalized',
ax=ax2, color=['#90CDBC', '#991857'])
In [24]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
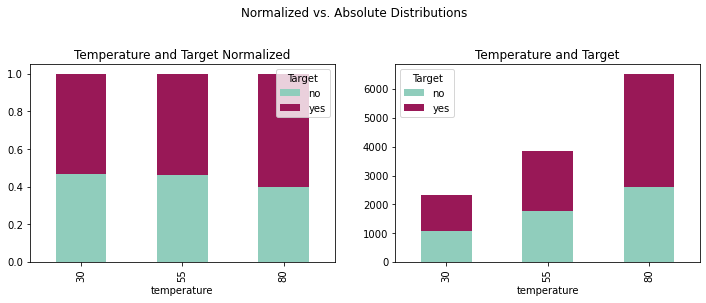
crosstabtemp = pd.crosstab(coupons_df['temperature'],coupons_df['Target'])
crosstabtempnorm = crosstabtemp.div(crosstabtemp.sum(1), axis = 0)
plottemp = crosstabtemp.plot(kind='bar', stacked = True,
title = 'Temperature and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plottempnorm = crosstabtempnorm.plot(kind='bar', stacked = True,
title = 'Temperature and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [25]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
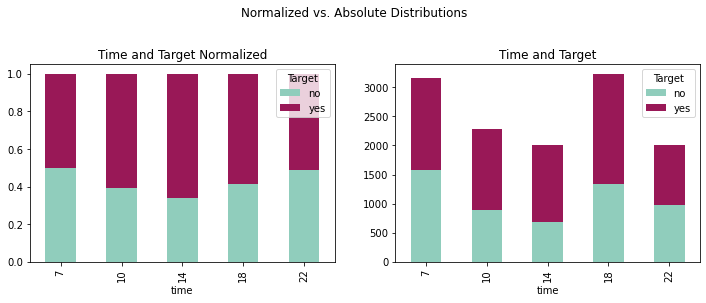
crosstabtime = pd.crosstab(coupons_df['time'],coupons_df['Target'])
crosstabtimenorm = crosstabtime.div(crosstabtime.sum(1), axis = 0)
plottime = crosstabtime.plot(kind='bar',
stacked=True,
title='Time and Target',
ax=ax1,
color=['#90CDBC', '#991857'])
plottimenorm = crosstabtimenorm.plot(kind='bar',
stacked=True,
title='Time and Target Normalized',
ax=ax2,
color=['#90CDBC', '#991857'])
In [26]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
# fig.suptitle('Normalized vs. Absolute Distributions')
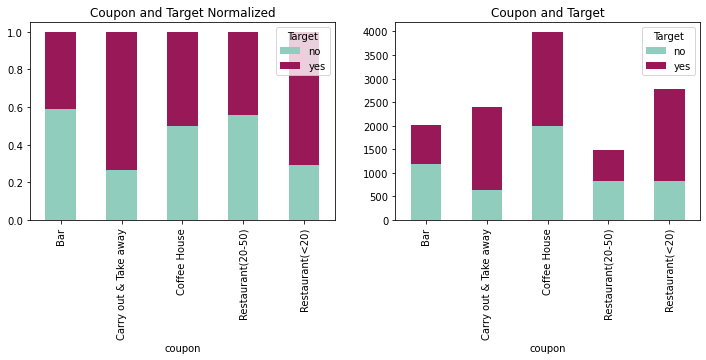
crosstabcoup = pd.crosstab(coupons_df['coupon'],coupons_df['Target'])
crosstabcoupnorm = crosstabcoup.div(crosstabcoup.sum(1), axis = 0)
plotcoup = crosstabcoup.plot(kind='bar', stacked = True,
title = 'Coupon and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plotcoupnorm = crosstabcoupnorm.plot(kind='bar', stacked = True,
title = 'Coupon and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [27]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221); ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
crosstabexpi = pd.crosstab(coupons_df['expiration'],coupons_df['Target'])
crosstabexpinorm = crosstabexpi.div(crosstabexpi.sum(1), axis = 0)
plotexpi = crosstabexpi.plot(kind='bar', stacked = True,
title = 'Expiration and Target', ax = ax1,
color = ['#90CDBC', '#991857'])
plotexpinorm = crosstabexpinorm.plot(kind='bar', stacked = True,
title = 'Expiration and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [28]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
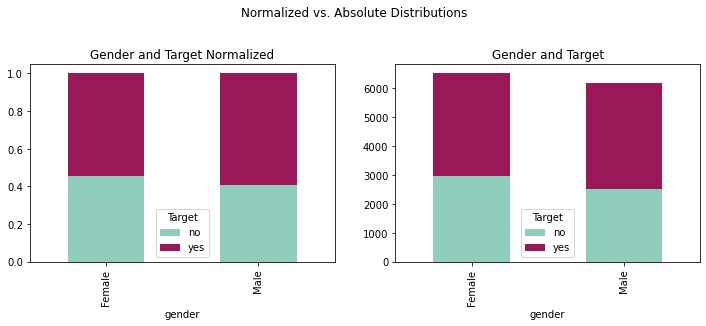
crosstabgender = pd.crosstab(coupons_df['gender'],coupons_df['Target'])
crosstabgendernorm = crosstabgender.div(crosstabgender.sum(1), axis = 0)
plotgender = crosstabgender.plot(kind='bar', stacked = True,
title = 'Gender and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plotgendernorm = crosstabgendernorm.plot(kind='bar', stacked = True,
title = 'Gender and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [29]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
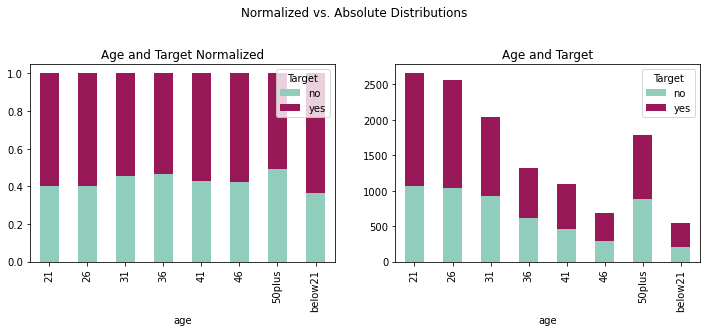
crosstabage = pd.crosstab(coupons_df['age'],coupons_df['Target'])
crosstabagenorm = crosstabage.div(crosstabage.sum(1), axis = 0)
plotage = crosstabage.plot(kind='bar', stacked = True,
title = 'Age and Target', ax = ax1,
color = ['#90CDBC', '#991857'])
plotagenorm = crosstabagenorm.plot(kind='bar', stacked = True,
title = 'Age and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [30]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221); ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
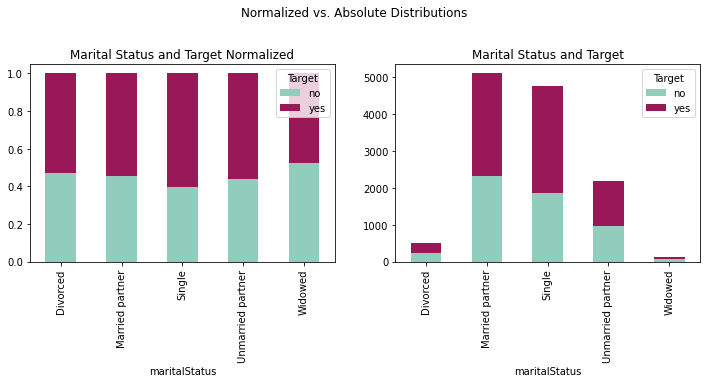
crosstabmari = pd.crosstab(coupons_df['maritalStatus'],coupons_df['Target'])
crosstabmarinorm = crosstabmari.div(crosstabmari.sum(1), axis=0)
plotmari = crosstabmari.plot(kind='bar', stacked=True,
title='Marital Status and Target',
ax=ax1, color=['#90CDBC', '#991857'])
plotmarinorm = crosstabmarinorm.plot(kind='bar', stacked = True,
title='Marital Status and Target Normalized',
ax=ax2, color=['#90CDBC', '#991857'])
In [31]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221); ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
crosstabchild = pd.crosstab(coupons_df['has_children'],
coupons_df['Target'])
crosstabchildnorm = crosstabchild.div(crosstabchild.sum(1), axis=0)
plotchild = crosstabchild.plot(kind='bar', stacked=True,
title='Child Status and Target',
ax=ax1, color=['#90CDBC', '#991857'])
plotchildnorm = crosstabchildnorm.plot(kind='bar', stacked=True,
title='Child Status and Target Normalized',
ax=ax2, color=['#90CDBC', '#991857'])
In [32]:
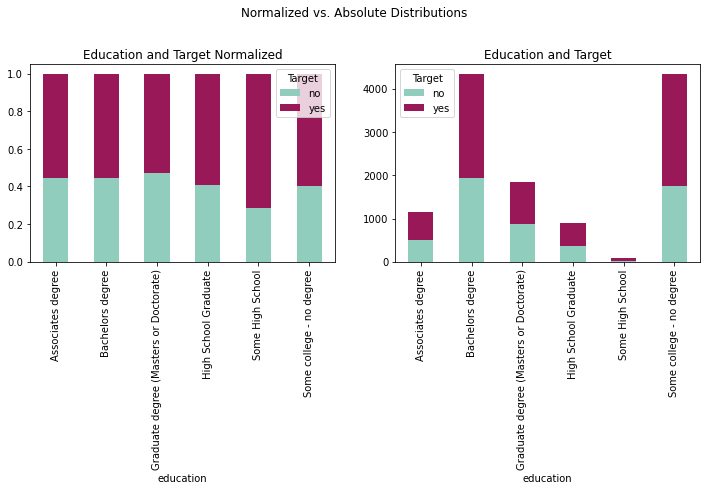
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
crosstabeduc = pd.crosstab(coupons_df['education'],coupons_df['Target'])
crosstabeducnorm = crosstabeduc.div(crosstabeduc.sum(1), axis = 0)
ploteduc = crosstabeduc.plot(kind='bar', stacked = True,
title = 'Education and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
ploteducnorm = crosstabeducnorm.plot(kind='bar', stacked = True,
title = 'Education and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [33]:
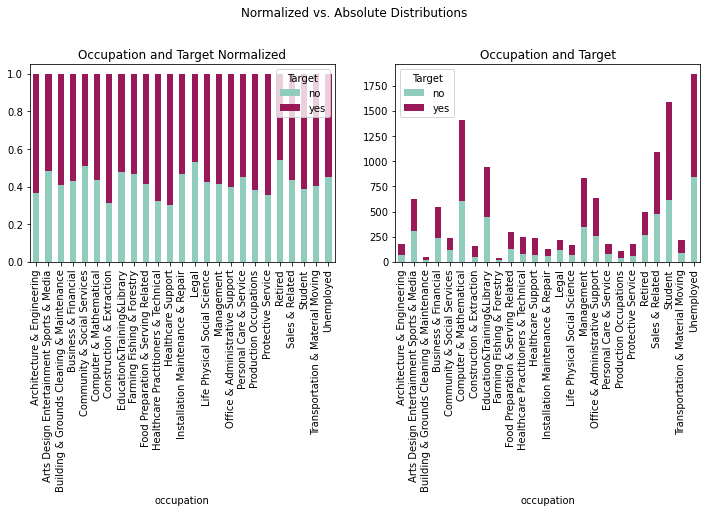
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
crosstaboccu = pd.crosstab(coupons_df['occupation'],coupons_df['Target'])
crosstaboccunorm = crosstaboccu.div(crosstaboccu.sum(1), axis = 0)
plotoccu = crosstaboccu.plot(kind='bar', stacked = True,
title = 'Occupation and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plotoccunorm = crosstaboccunorm.plot(kind='bar', stacked = True,
title = 'Occupation and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [34]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
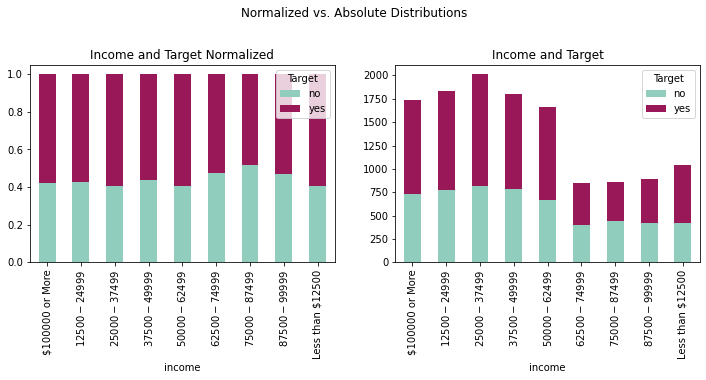
crosstabinco = pd.crosstab(coupons_df['income'],
coupons_df['Target'])
crosstabinconorm = crosstabinco.div(crosstabinco.sum(1), axis = 0)
plotinco = crosstabinco.plot(kind='bar', stacked = True,
title = 'Income and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plotinconorm = crosstabinconorm.plot(kind='bar', stacked = True,
title = 'Income and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [35]:
fig = plt.figure(figsize=(12, 8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
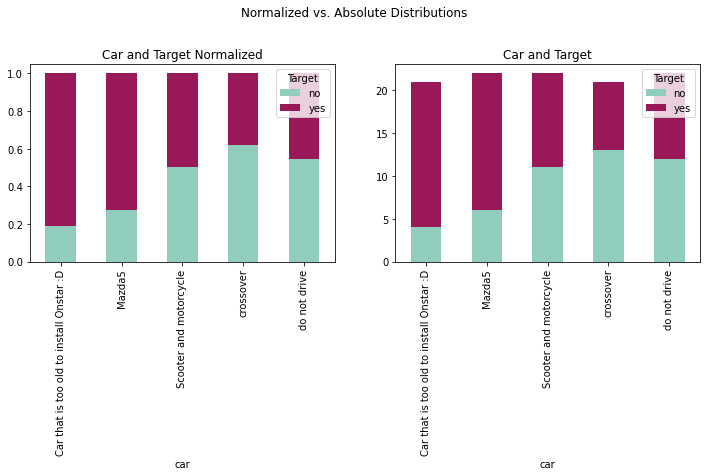
crosstabcar = pd.crosstab(coupons_df['car'],coupons_df['Target'])
crosstabcarnorm = crosstabcar.div(crosstabcar.sum(1),
axis = 0)
plotcar = crosstabcar.plot(kind='bar',
stacked=True,
title='Car and Target',
ax=ax1,
color=['#90CDBC', '#991857'])
plotcarnorm = crosstabcarnorm.plot(kind='bar',
stacked=True,
title='Car and Target Normalized',
ax=ax2,
color=['#90CDBC',
'#991857'])
In [36]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
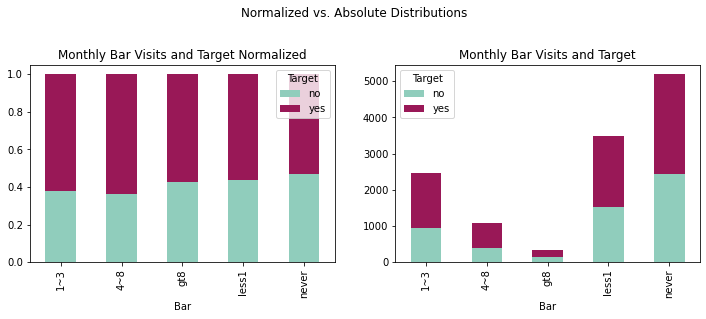
crosstabbar = pd.crosstab(coupons_df['Bar'], coupons_df['Target'])
crosstabbarnorm = crosstabbar.div(crosstabbar.sum(1),
axis=0)
plotbar = crosstabbar.plot(kind='bar',
stacked=True,
title='Monthly Bar Visits and Target',
ax=ax1,
color=['#90CDBC',
'#991857'])
plotbarnorm = crosstabbarnorm.plot(kind='bar', stacked = True,
title='Monthly Bar Visits and Target ' +
'Normalized',
ax=ax2,
color=['#90CDBC',
'#991857'])
In [37]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221); ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
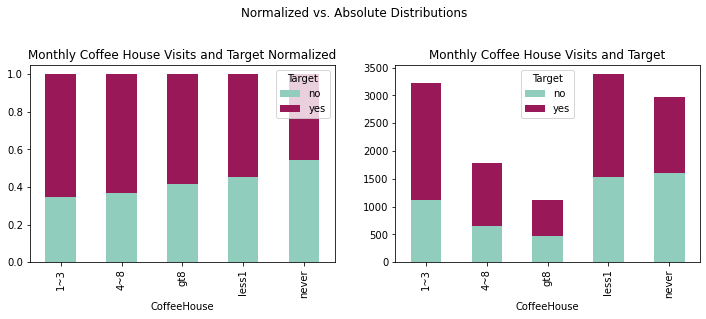
crosstabcoff = pd.crosstab(coupons_df['CoffeeHouse'], coupons_df['Target'])
crosstabcoffnorm = crosstabcoff.div(crosstabcoff.sum(1), axis = 0)
plotcoff = crosstabcoff.plot(kind='bar', stacked=True,
title='Monthly Coffee House Visits and Target',
ax=ax1, color=['#90CDBC', '#991857'])
plotcoffnorm = crosstabcoffnorm.plot(kind='bar', stacked=True,
title = 'Monthly Coffee House Visits and Target Normalized',
ax=ax2, color=['#90CDBC', '#991857'])
In [38]:
fig = plt.figure(figsize=(12,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
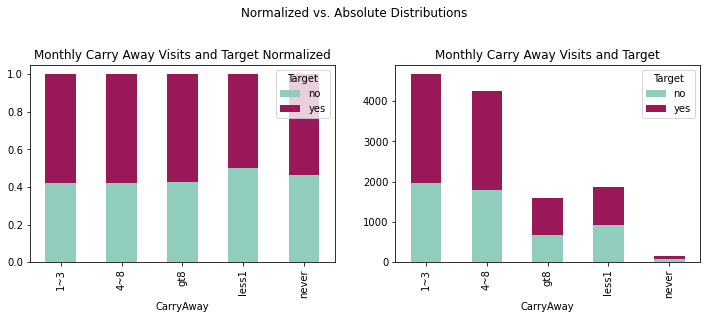
crosstabcarr = pd.crosstab(coupons_df['CarryAway'],coupons_df['Target'])
crosstabcarrnorm = crosstabcarr.div(crosstabcarr.sum(1), axis = 0)
plotcarr = crosstabcarr.plot(kind='bar', stacked = True,
title = 'Monthly Carry Away Visits and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plotcarrnorm = crosstabcarrnorm.plot(kind='bar', stacked = True,
title = 'Monthly Carry Away Visits and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [39]:
fig = plt.figure(figsize=(14,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
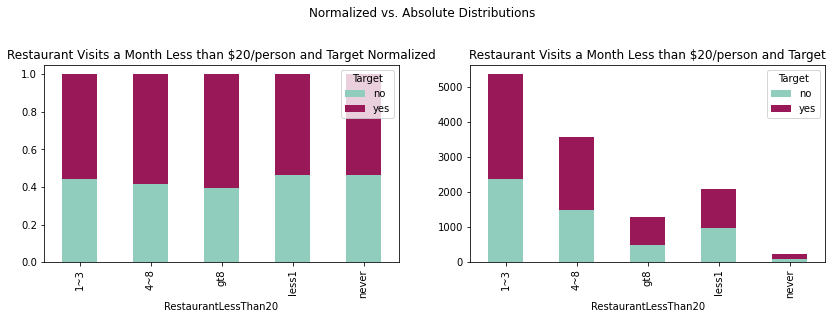
crosstabLess = pd.crosstab(coupons_df['RestaurantLessThan20'],coupons_df['Target'])
crosstabLessnorm = crosstabLess.div(crosstabLess.sum(1), axis = 0)
plotLess = crosstabLess.plot(kind='bar', stacked = True,
title = 'Restaurant Visits a Month Less than $20/person and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plotLessnorm = crosstabLessnorm.plot(kind='bar', stacked = True,
title = 'Restaurant Visits a Month Less than $20/person and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [40]:
fig = plt.figure(figsize=(14,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
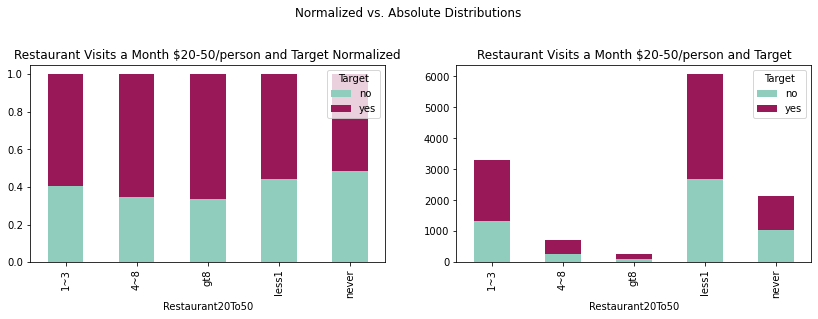
crosstabTo50 = pd.crosstab(coupons_df['Restaurant20To50'],coupons_df['Target'])
crosstabTo50norm = crosstabTo50.div(crosstabTo50.sum(1), axis = 0)
plotTo50 = crosstabTo50.plot(kind='bar', stacked = True,
title = 'Restaurant Visits a Month $20-50/person and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plotTo50norm = crosstabTo50norm.plot(kind='bar', stacked = True,
title = 'Restaurant Visits a Month $20-50/person and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [41]:
fig = plt.figure(figsize=(14,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
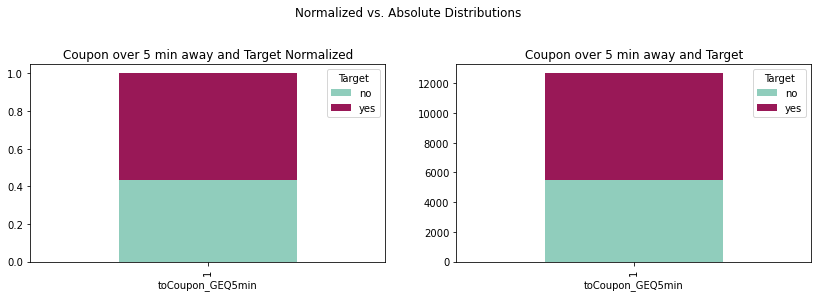
crosstab5min = pd.crosstab(coupons_df['toCoupon_GEQ5min'],coupons_df['Target'])
crosstab5minnorm = crosstab5min.div(crosstab5min.sum(1), axis = 0)
plot5min = crosstab5min.plot(kind='bar', stacked = True,
title = 'Coupon over 5 min away and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plot5minnorm = crosstab5minnorm.plot(kind='bar', stacked = True,
title = 'Coupon over 5 min away and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [42]:
fig = plt.figure(figsize=(14,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
crosstab15min = pd.crosstab(coupons_df['toCoupon_GEQ15min'],
coupons_df['Target'])
crosstab15minnorm = crosstab15min.div(crosstab15min.sum(1),
axis = 0)
plot15min = crosstab15min.plot(kind='bar',
stacked = True,
title = 'Coupon over 15 min away and Target',
ax = ax1,
color = ['#90CDBC', '#991857'])
plot15minnorm = crosstab15minnorm.plot(kind='bar',
stacked = True,
title = 'Coupon over 15 min away and Target Normalized',
ax = ax2,
color = ['#90CDBC', '#991857'])
In [43]:
fig = plt.figure(figsize=(14,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
crosstab25min = pd.crosstab(coupons_df['toCoupon_GEQ25min'],coupons_df['Target'])
crosstab25minnorm = crosstab25min.div(crosstab25min.sum(1), axis = 0)
plot25min = crosstab25min.plot(kind='bar', stacked = True,
title = 'Coupon over 25 min away and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plot25minnorm = crosstab25minnorm.plot(kind='bar', stacked = True,
title = 'Coupon over 25 min away and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
In [44]:
fig = plt.figure(figsize=(14,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
crosstabsame = pd.crosstab(coupons_df['direction_same'],
coupons_df['Target'])
crosstabsamenorm = crosstabsame.div(crosstabsame.sum(1),
axis = 0)
plotsame = crosstabsame.plot(kind='bar',
stacked = True,
title = 'Coupon Same Direction and Target',
ax = ax1,
color = ['#90CDBC', '#991857'])
plotsamenorm = crosstabsamenorm.plot(kind='bar',
stacked = True,
title = 'Coupon Same Direction and Target Normalized',
ax = ax2,
color = ['#90CDBC', '#991857'])
In [45]:
fig = plt.figure(figsize=(14,8))
ax2 = fig.add_subplot(221)
ax1 = fig.add_subplot(222)
fig.suptitle('Normalized vs. Absolute Distributions')
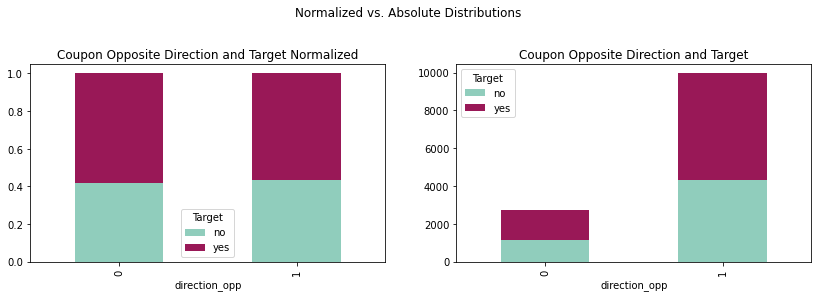
crosstabopp = pd.crosstab(coupons_df['direction_opp'],coupons_df['Target'])
crosstaboppnorm = crosstabopp.div(crosstabopp.sum(1), axis = 0)
plotopp = crosstabopp.plot(kind='bar', stacked = True,
title = 'Coupon Opposite Direction and Target',
ax = ax1, color = ['#90CDBC', '#991857'])
plotoppnorm = crosstaboppnorm.plot(kind='bar', stacked = True,
title = 'Coupon Opposite Direction and Target Normalized',
ax = ax2, color = ['#90CDBC', '#991857'])
Dropping Unnecessary Columns
With a 99.15% missing percentage, any imputation method would be impractical and the variable car will be dropped
Since 'toCoupon_GEQ5min Column' is a constant feature, we remove it.
Since 'direction_opp' is a highly correlated variable, it is dropped as well.
In [46]:
coupons_df.drop(columns=['car'], inplace=True)
In [47]:
coupons_df.drop(columns=['toCoupon_GEQ5min'], inplace=True)
In [48]:
coupons_df.drop(columns=['direction_opp'], inplace=True)
Examining Correlations¶
In [49]:
corr = coupons_df.corr()
corr.style.background_gradient(cmap='coolwarm')
Out[49]:
Evaluation of Imputation Methods¶
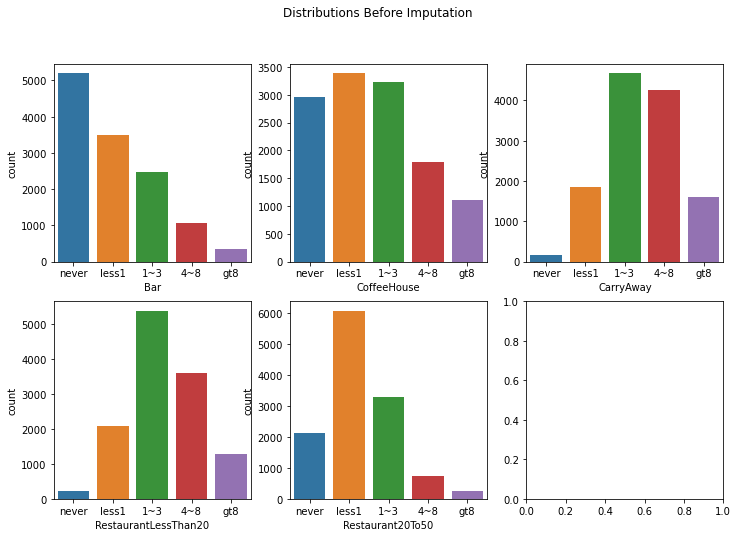
The variables Bar, CoffeeHouse, CarryAway, RestaurantLessThan20, Restaurant20To50, have a low null count $ < 2\%$. We will evaluate different imputation methods that best preserves the distribution of the data.
In [50]:
fig, axes = plt.subplots(2, 3, figsize=(12, 8))
likert_vals = ['never', 'less1', '1~3', '4~8', 'gt8']
fig.suptitle('Distributions Before Imputation')
sns.countplot(ax=axes[0, 0], data=coupons_df,
x="Bar", order=likert_vals)
sns.countplot(ax=axes[0, 1], data=coupons_df,
x="CoffeeHouse", order=likert_vals)
sns.countplot(ax=axes[0, 2], data=coupons_df,
x="CarryAway", order=likert_vals)
sns.countplot(ax=axes[1, 0], data=coupons_df,
x="RestaurantLessThan20", order=likert_vals)
sns.countplot(ax=axes[1, 1], data=coupons_df,
x="Restaurant20To50", order=likert_vals)
plt.show()
KL Divergence¶
The Kullback-Leibler Divergence will be used to determine the amount the distribution of each variable diverges after imputation. The imputation method with the smallest KL divergence will be selected.
$$ D_{KL}(P||Q) = \Large\sum_{i}\normalsize P(i) \normalsize\text{log}\frac{P(i)}{Q(i)}$$$$ D_{KL}(P||Q) = \Large \int \normalsize P(x) \normalsize\text{log}\frac{P(x)}{Q(x)} dx$$
In [51]:
def kl_divergence(p, q):
return sum(p * np.log(p/q))
Imputation Methods¶
- Median Imputation
- Frequent Imputation
The values of the variables Bar, CoffeeHouse, CarryAway, RestaurantLessThan20, Restaurant20To50, appear to be values from a likert scale. These are ordinal values, so they will be converted accordingly, before median imputation can be used.
In [52]:
impute_test = coupons_df[['Bar', 'CoffeeHouse', 'CarryAway',
'RestaurantLessThan20', 'Restaurant20To50']]
impute_test.replace({'never': 0, 'less1': 1, '1~3': 2, '4~8': 3, 'gt8': 4},
inplace=True)
# Store KL results
cols = ['Bar', 'CoffeeHouse', 'CarryAway', 'RestaurantLessThan20',
'Restaurant20To50']
kl_results = pd.DataFrame(index=cols)
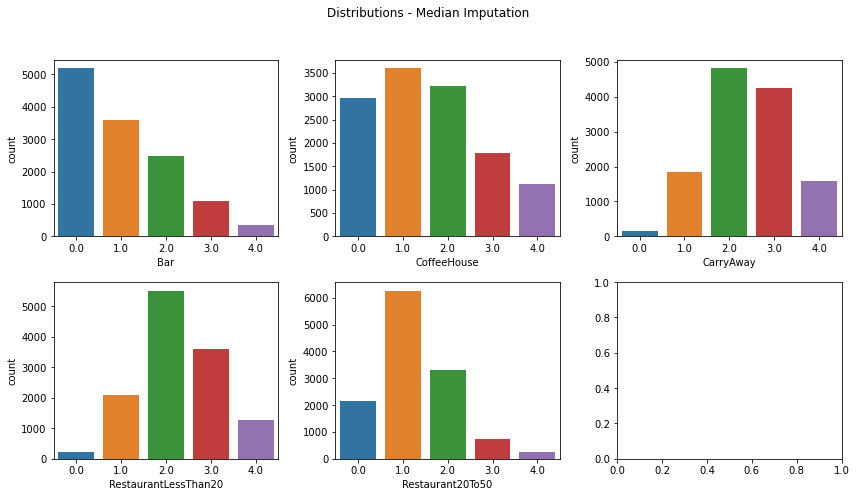
Median Imputation
In [53]:
med_impute = SimpleImputer(missing_values=np.nan, strategy='median')
med_impute_df = pd.DataFrame(med_impute.fit_transform(impute_test),
columns=['Bar', 'CoffeeHouse', 'CarryAway',
'RestaurantLessThan20', 'Restaurant20To50'])
In [54]:
fig, axes = plt.subplots(2, 3, figsize=(12, 7))
fig.suptitle('Distributions - Median Imputation')
sns.countplot(ax=axes[0, 0], data=med_impute_df, x="Bar")
sns.countplot(ax=axes[0, 1], data=med_impute_df, x="CoffeeHouse")
sns.countplot(ax=axes[0, 2], data=med_impute_df, x="CarryAway")
sns.countplot(ax=axes[1, 0], data=med_impute_df, x="RestaurantLessThan20")
sns.countplot(ax=axes[1, 1], data=med_impute_df, x="Restaurant20To50")
plt.tight_layout(rect=[0, 0, 1, 0.9]); plt.show()
In [55]:
med_results = []
for col in cols:
p = impute_test[col].dropna()
p = p.groupby(p).count() / p.shape[0]
q = med_impute_df[col].groupby(med_impute_df[col]).count() / \
med_impute_df[col].shape[0]
print('P(%s = x) = %s' % (col, p.to_list()))
print('Q(%s = x) = %s' % (col, q.to_list()))
print('KL Divergence: %f' % kl_divergence(p, q))
print('\n')
med_results.append(kl_divergence(p, q))
kl_results['Median Imputation'] = med_results
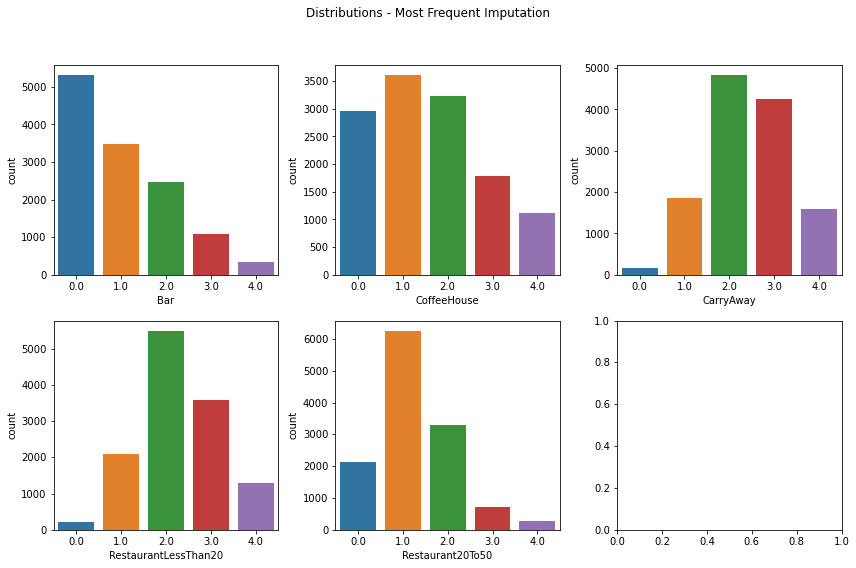
Frequent Imputation
In [56]:
freq_impute = SimpleImputer(missing_values=np.nan, strategy='most_frequent')
freq_impute_df = pd.DataFrame(freq_impute.fit_transform(impute_test),
columns=['Bar', 'CoffeeHouse', 'CarryAway',
'RestaurantLessThan20', 'Restaurant20To50'])
In [57]:
fig, axes = plt.subplots(2, 3, figsize=(12, 8))
fig.suptitle('Distributions - Most Frequent Imputation')
sns.countplot(ax=axes[0, 0], data=freq_impute_df, x="Bar")
sns.countplot(ax=axes[0, 1], data=freq_impute_df, x="CoffeeHouse")
sns.countplot(ax=axes[0, 2], data=freq_impute_df, x="CarryAway")
sns.countplot(ax=axes[1, 0], data=freq_impute_df, x="RestaurantLessThan20")
sns.countplot(ax=axes[1, 1], data=freq_impute_df, x="Restaurant20To50")
plt.tight_layout(rect=[0, 0, 1, 0.9]); plt.show()
In [58]:
freq_results = []
for col in cols:
p = impute_test[col].dropna()
p = p.groupby(p).count() / p.shape[0]
q = freq_impute_df[col].groupby(freq_impute_df[col]).count() / \
freq_impute_df[col].shape[0]
print('P(%s = x) = %s' % (col, p.to_list()))
print('Q(%s = x) = %s' % (col, q.to_list()))
print('KL Divergence: %f' % kl_divergence(p, q))
print('\n')
freq_results.append(kl_divergence(p, q))
kl_results['Frequent Imputation'] = freq_results
KL Divergence of Imputation Methods¶
In [59]:
kl_results
Out[59]:
As shown in the table above, the imputation methods are almost identical with Imputation by Most Frequent Value (Mode) having a slightly lower KL Divergence for the variable Bar. Imputation by Most Frequent Value will be used.
Imputation by Most Frequent Value¶
In [60]:
# replace values of Bar, CoffeeHouse, CarryAway,
# RestaurantLessThan20, Restaurant20To50 as ordinal
coupons_df[cols] = coupons_df[cols].replace({'never': 0,
'less1': 1, '1~3': 2,
'4~8': 3, 'gt8': 4})
coupons_df[cols] = SimpleImputer(missing_values=np.nan,
strategy='most_frequent').fit_transform(coupons_df[cols])
In [61]:
null_vals = pd.DataFrame(coupons_df.isna().sum(), columns=['Null Count'])
null_vals['Null Percent'] = (null_vals['Null Count'] / coupons_df.shape[0]) * 100
null_vals
Out[61]:
Preprocessing¶
In [62]:
coupons_df = pd.read_csv('https://archive.ics.uci.edu/ml/\
machine-learning-databases/00603/in-vehicle-coupon-recommendation.csv')
coupons_df.head()
Out[62]:
In [63]:
# define columns types
nom = ['destination', 'passenger', 'weather', 'coupon',
'gender', 'maritalStatus', 'occupation']
bin = ['gender', 'has_children', 'toCoupon_GEQ15min',
'toCoupon_GEQ25min', 'direction_same']
ord = ['temperature', 'age', 'education', 'income',
'Bar', 'CoffeeHouse', 'CarryAway', 'RestaurantLessThan20',
'Restaurant20To50']
num = ['time', 'expiration']
ex = ['car', 'toCoupon_GEQ5min', 'direction_opp']
In [64]:
# Convert time to 24h military time
def convert_time(x):
if x[-2:] == "AM":
return int(x[0:-2]) % 12
else:
return (int(x[0:-2]) % 12) + 12
def average_income(x):
inc = np.array(x).astype(np.float)
return sum(inc) / len(inc)
def pre_process(df):
# keep original dataframe imutable
ret = df.copy()
# Drop columns
ret.drop(columns=['car', 'toCoupon_GEQ5min', 'direction_opp'],
inplace=True)
# rename values
ret = ret.rename(columns={'passanger':'passenger'})
ret['time'] = ret['time'].apply(convert_time)
ret['expiration'] = ret['expiration'].map({'1d':24, '2h':2})
# convert the following columns to ordinal values
ord_cols = ['Bar', 'CoffeeHouse', 'CarryAway', 'RestaurantLessThan20',
'Restaurant20To50']
ret[ord_cols] = ret[ord_cols].replace({'never': 0, 'less1': 1,
'1~3': 2, '4~8': 3, 'gt8': 4})
# impute missing
ret[ord_cols] = SimpleImputer(missing_values=np.nan,
strategy='most_frequent').fit_transform(ret[ord_cols])
# Changing coupon expiration to uniform # of hours
ret['expiration'] = coupons_df['expiration'].map({'1d':24, '2h':2})
# Age, Education, Income as ordinal
ret['age'] = ret['age'].map({'below21':1,
'21':2,'26':3,
'31':4,'36':5,
'41':6,'46':6,
'50plus':7})
ret['education'] = ret['education'].map(\
{'Some High School':1,
'Some college - no degree':2,
'Bachelors degree':3, 'Associates degree':4,
'High School Graduate':5,
'Graduate degree (Masters or Doctorate)':6})
ret['average income'] = ret['income'].str.findall('(\d+)').apply(average_income)
ret['income'].replace({'Less than $12500': 1, '$12500 - $24999': 2,
'$25000 - $37499': 3, '$37500 - $49999': 4,
'$50000 - $62499': 5, '$62500 - $74999': 6,
'$75000 - $87499': 7, '$87500 - $99999': 8,
'$100000 or More': 9}, inplace=True)
# Change gender to binary value
ret['gender'].replace({'Male': 0, 'Female': 1}, inplace=True)
# One Hot Encode
nom = ['destination', 'passenger', 'weather', 'coupon',
'maritalStatus', 'occupation']
for col in nom:
# k-1 cols from k values
ohe_cols = pd.get_dummies(ret[col], prefix=col, drop_first=True)
ret = pd.concat([ret, ohe_cols], axis=1)
ret.drop(columns=[col], inplace=True)
return ret
In [65]:
# Simple function to prep a dataframe for a model
def scale_data(df, std, norm, pass_cols):
"""
df: raw dataframe you want to process
std: list of column names you want to standardize (0 mean unit variance)
norm: list of column names you want to normalize (min-max)
pass_cols: list of columns that do not require processing (target var, etc.)
returns: prepped dataframe
"""
ret = df.copy()
# Only include columns from lists
ret = ret[std + norm + pass_cols]
# Standardize scaling for gaussian features
if (isinstance(std, list)) and (len(std) > 0):
ret[std] = StandardScaler().fit(ret[std]).transform(ret[std])
# Normalize (min-max) [0,1] for non-gaussian features
if (isinstance(norm, list)) and (len(norm) > 0):
ret[norm] = Normalizer().fit(ret[norm]).transform(ret[norm])
return ret
In [66]:
# Processed data (remove labels from dataset)
coupons_proc = pre_process(coupons_df.drop(columns='Y'))
# Labels
labels = coupons_df['Y']
# Standardize/Normalize
to_scale = ['average income', 'temperature', 'time', 'expiration']
coupons_proc = scale_data(coupons_proc, to_scale, [],
list(set(coupons_proc.columns.tolist()).difference(set(to_scale))))
coupons_proc.head()
Out[66]:
In [67]:
coupons_df
Out[67]:
Selecting Predictors for Modeling¶
In [68]:
X = pd.DataFrame(coupons_proc[['average income', 'education', 'expiration',
'age','temperature','has_children']])
Generalized Linear Model¶
$$ y = \beta_0 + \beta_1x_1 +\beta_2x_2 +\cdots+\beta_px_p + \varepsilon $$
Logistic Regression¶
Link Function for Binary Response¶
$$ X\beta = \text{ln} \frac{\mu}{1-\mu} $$where $e^{\text{ln}(x)}=x$ and,
$$ \mu = \frac{e^{X\beta}}{1+e^{X\beta}} $$Logistic Regression - Parametric Form¶
$$p(y) = \frac{\text{exp}(\beta_0+\beta_1x_1+\beta_2x_2+\cdot\cdot\cdot+\beta_px_p)}{1+\text{exp}(\beta_0+\beta_1x_1+\beta_2x_2+\cdot\cdot\cdot+\beta_px_p)} + \varepsilon$$
Logistic Regression - Descriptive Form¶
$$\hat{p}(y) = \frac{\text{exp}(b_0+b_1x_1+b_2x_2+\cdot\cdot\cdot+b_px_p)}{1+\text{exp}(b_0+b_1x_1+b_2x_2+\cdot\cdot\cdot+b_px_p)}$$
$$\hat{p}(\text{coupons}) = \frac{\text{exp}(b_0+b_1(\text{average income})+b_2(\text{education})+\cdot\cdot\cdot+b_px_p))}{1+\text{exp}(b_0+b_1(\text{average income})+b_2(\text{education})+\cdot\cdot\cdot+b_px_p))}$$
In [69]:
X = sm.add_constant(X)
y = pd.DataFrame(coupons_df[['Y']])
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.20, random_state=42)
log_results = sm.Logit(y_train, X_train).fit()
log_results.summary()
Out[69]:
Whether or not an individual has children bears no statistical significance for this baseline model at a p-value of 0.107. Thus, we omit this predictor from this model.
That being said, we will explore re-introducing these for subsequent models
In [70]:
X = pd.DataFrame(coupons_proc[['average income', 'education', 'expiration',
'temperature','has_children']])
The refined logistic regression equation becomes:
$\small{\hat{p}(\text{coupons}) = \frac{\text{exp}(0.0147-0.000001821(\text{average income})-0.0512(\text{education})+0.0262(\text{expiration})-0.0053(\text{age})+0.0079(\text{temperature}))}{1+\text{exp}(0.0147-0.000001821(\text{average income})-0.0512(\text{education})+0.0262(\text{expiration})-0.0053(\text{age})+0.0079(\text{temperature}))}}$
In [71]:
logreg = LogisticRegression()
logreg.fit(X_train, y_train)
y_pred = logreg.predict(X_test)
pred_log = [round(num) for num in y_pred]
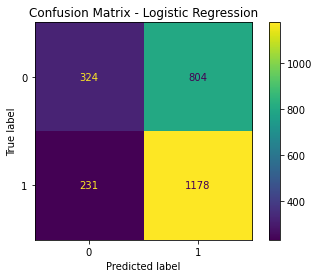
confusion_matrix(y_test, pred_log)
Out[71]:
In [72]:
plot_confusion_matrix(logreg, X_test, y_test)
plt.title('Confusion Matrix - Logistic Regression')
plt.show()
In [73]:
print(classification_report(y_test, y_pred))
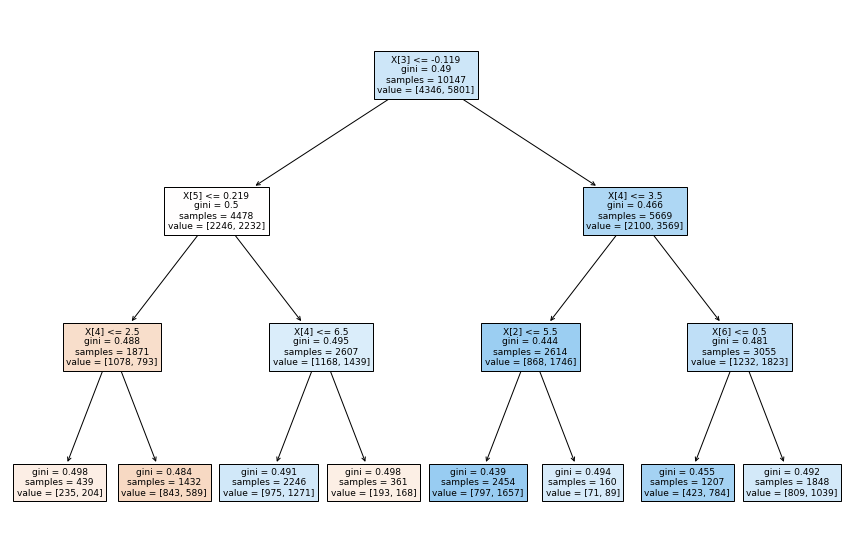
Decision Tree Classifier¶
In [74]:
coupon_tree = tree.DecisionTreeClassifier(max_depth=3)
coupon_tree = coupon_tree.fit(X_train,y_train)
y_pred = coupon_tree.predict(X_test)
print('accuracy %2.2f ' % accuracy_score(y_test,y_pred))
In [75]:
print(classification_report(y_test, y_pred))
In [76]:
fig, ax = plt.subplots(figsize = (15, 10))
short_treeplot = tree.plot_tree(coupon_tree, filled=True)
plt.tight_layout(rect=[0, 0, 0, 0])
plt.show()
